Soft Actor-Critic (SAC)
Overview
The Soft Actor-Critic (SAC) algorithm extends the DDPG algorithm by 1) using a stochastic policy, which in theory can express multi-modal optimal policies. This also enables the use of 2) entropy regularization based on the stochastic policy's entropy. It serves as a built-in, state-dependent exploration heuristic for the agent, instead of relying on non-correlated noise processes as in DDPG, or TD3 Additionally, it incorporates the 3) usage of two Soft Q-network to reduce the overestimation bias issue in Q-network-based methods.
Original papers: The SAC algorithm's initial proposal, and later updates and improvements can be chronologically traced through the following publications:
- Reinforcement Learning with Deep Energy-Based Policies
- Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
- Composable Deep Reinforcement Learning for Robotic Manipulation
- Soft Actor-Critic Algorithms and Applications
- Soft Actor-Critic for Discrete Action Settings (No peer review, preprint only)
Reference resources:
- haarnoja/sac
- openai/spinningup
- pranz24/pytorch-soft-actor-critic
- DLR-RM/stable-baselines3
- denisyarats/pytorch_sac
- haarnoja/softqlearning
- rail-berkeley/softlearning
- p-christ/Deep-Reinforcement-Learning-Algorithms-with-PyTorch
- toshikwa/sac-discrete.pytorch
| Variants Implemented | Description |
|---|---|
sac_continuous_actions.py, docs |
For continuous action spaces |
sac_atari.py, docs |
For discrete action spaces |
Below are our single-file implementations of SAC:
sac_continuous_action.py
The sac_continuous_action.py has the following features:
- For continuous action spaces.
- Works with the
Boxobservation space of low-level features. - Works with the
Box(continuous) action space. - Numerically stable stochastic policy based on openai/spinningup and pranz24/pytorch-soft-actor-critic implementations.
- Supports automatic entropy coefficient \(\alpha\) tuning, enabled by default.
Usage for continuous action spaces
poetry install
poetry install -E mujoco
poetry run python cleanrl/sac_continuous_action.py --help
poetry run python cleanrl/sac_continuous_action.py --env-id Hopper-v4
poetry install -E mujoco_py # only works in Linux
poetry run python cleanrl/sac_continuous_action.py --env-id Hopper-v2
poetry run python cleanrl/sac_continuous_action.py --env-id Hopper-v2 --autotune False --alpha 0.2 ## Without Automatic entropy coef. tuning
pip install -r requirements/requirements-mujoco.txt
python cleanrl/sac_continuous_action.py --help
python cleanrl/sac_continuous_action.py --env-id Mujoco-v4
pip install -r requirements/requirements-mujoco_py.txt # only works in Linux
python cleanrl/sac_continuous_action.py --env-id Hopper-v2
python cleanrl/sac_continuous_action.py --env-id Hopper-v2 --autotune False --alpha 0.2 ## Without Automatic entropy coef. tuning
Explanation of the logged metrics
Running python cleanrl/sac_continuous_action.py will automatically record various metrics such as actor or value losses in Tensorboard. Below is the documentation for these metrics:
-
charts/episodic_return: the episodic return of the game during training -
charts/SPS: number of steps per second -
losses/qf1_loss,losses/qf2_loss: for each Soft Q-value network \(Q_{\theta_i}\), \(i \in \{1,2\}\), this metric holds the mean squared error (MSE) between the soft Q-value estimate \(Q_{\theta_i}(s, a)\) and the entropy regularized Bellman update target estimated as \(r_t + \gamma \, Q_{\theta_{i}^{'}}(s', a') + \alpha \, \mathcal{H} \big[ \pi(a' \vert s') \big]\).
More formally, the Soft Q-value loss for the \(i\)-th network is obtained by:
with the entropy regularized, Soft Bellman update target: $$ y = r(s, a) + \gamma ({\color{orange} \min_{\theta_{1,2}}Q_{\theta_i^{'}}(s',a')} - \alpha \, \text{log} \pi( \cdot \vert s')) $$ where \(a' \sim \pi( \cdot \vert s')\), \(\text{log} \pi( \cdot \vert s')\) approximates the entropy of the policy, and \(\mathcal{D}\) is the replay buffer storing samples of the agent during training.
Here, \(\min_{\theta_{1,2}}Q_{\theta_i^{'}}(s',a')\) takes the minimum Soft Q-value network estimate between the two target Q-value networks \(Q_{\theta_1^{'}}\) and \(Q_{\theta_2^{'}}\) for the next state and action pair, so as to reduce over-estimation bias.
-
losses/qf_loss: averageslosses/qf1_lossandlosses/qf2_lossfor comparison with algorithms using a single Q-value network. -
losses/actor_loss: Given the stochastic nature of the policy in SAC, the actor (or policy) objective is formulated so as to maximize the likelihood of actions \(a \sim \pi( \cdot \vert s)\) that would result in high Q-value estimate \(Q(s, a)\). Additionally, the policy objective encourages the policy to maintain its entropy high enough to help explore, discover, and capture multi-modal optimal policies.
The policy's objective function can thus be defined as:
where the action is sampled using the reparameterization trick1: \(a = \mu_{\phi}(s) + \epsilon \, \sigma_{\phi}(s)\) with \(\epsilon \sim \mathcal{N}(0, 1)\), \(\text{log} \pi_{\phi}( \cdot \vert s')\) approximates the entropy of the policy, and \(\mathcal{D}\) is the replay buffer storing samples of the agent during training.
-
losses/alpha: \(\alpha\) coefficient for entropy regularization of the policy. -
losses/alpha_loss: In the policy's objective defined above, the coefficient of the entropy bonus \(\alpha\) is kept fixed all across the training. As suggested by the authors in Section 5 of the Soft Actor-Critic And Applications paper, the original purpose of augmenting the standard reward with the entropy of the policy is to encourage exploration of not well enough explored states (thus high entropy). Conversely, for states where the policy has already learned a near-optimal policy, it would be preferable to reduce the entropy bonus of the policy, so that it does not become sub-optimal due to the entropy maximization incentive.
Therefore, having a fixed value for \(\alpha\) does not fit this desideratum of matching the entropy bonus with the knowledge of the policy at an arbitrary state during its training.
To mitigate this, the authors proposed a method to dynamically adjust \(\alpha\) as the policy is trained, which is as follows:
where \(\mathcal{H}\) represents the target entropy, the desired lower bound for the expected entropy of the policy over the trajectory distribution induced by the latter. As a heuristic for the target entropy, the authors use the dimension of the action space of the task.
Implementation details
CleanRL's sac_continuous_action.py implementation is based on openai/spinningup.
-
sac_continuous_action.pyuses a numerically stable estimation method for the standard deviation \(\sigma\) of the policy, which squashes it into a range of reasonable values for a standard deviation:LOG_STD_MAX = 2 LOG_STD_MIN = -5 class Actor(nn.Module): def __init__(self, env): super(Actor, self).__init__() self.fc1 = nn.Linear(np.array(env.single_observation_space.shape).prod(), 256) self.fc2 = nn.Linear(256, 256) self.fc_mean = nn.Linear(256, np.prod(env.single_action_space.shape)) self.fc_logstd = nn.Linear(256, np.prod(env.single_action_space.shape)) # action rescaling self.action_scale = torch.FloatTensor((env.action_space.high - env.action_space.low) / 2.0) self.action_bias = torch.FloatTensor((env.action_space.high + env.action_space.low) / 2.0) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) mean = self.fc_mean(x) log_std = self.fc_logstd(x) log_std = torch.tanh(log_std) log_std = LOG_STD_MIN + 0.5 * (LOG_STD_MAX - LOG_STD_MIN) * (log_std + 1) # From SpinUp / Denis Yarats return mean, log_std def get_action(self, x): mean, log_std = self(x) std = log_std.exp() normal = torch.distributions.Normal(mean, std) x_t = normal.rsample() # for reparameterization trick (mean + std * N(0,1)) y_t = torch.tanh(x_t) action = y_t * self.action_scale + self.action_bias log_prob = normal.log_prob(x_t) # Enforcing Action Bound log_prob -= torch.log(self.action_scale * (1 - y_t.pow(2)) + 1e-6) log_prob = log_prob.sum(1, keepdim=True) mean = torch.tanh(mean) * self.action_scale + self.action_bias return action, log_prob, mean def to(self, device): self.action_scale = self.action_scale.to(device) self.action_bias = self.action_bias.to(device) return super(Actor, self).to(device)Note that unlike openai/spinningup's implementation which uses
LOG_STD_MIN = -20, CleanRL's usesLOG_STD_MIN = -5instead. -
sac_continuous_action.pyuses different learning rates for the policy and the Soft Q-value networks optimization.parser.add_argument("--policy-lr", type=float, default=3e-4, help="the learning rate of the policy network optimizer") parser.add_argument("--q-lr", type=float, default=1e-3, help="the learning rate of the Q network network optimizer")while openai/spinningup's uses a single learning rate of
lr=1e-3for both components.Note that in case it is used, the automatic entropy coefficient \(\alpha\)'s tuning shares the
q-lrlearning rate:# Automatic entropy tuning if args.autotune: target_entropy = -torch.prod(torch.Tensor(envs.single_action_space.shape).to(device)).item() log_alpha = torch.zeros(1, requires_grad=True, device=device) alpha = log_alpha.exp().item() a_optimizer = optim.Adam([log_alpha], lr=args.q_lr) else: alpha = args.alpha -
sac_continuous_action.pyuses--batch-size=256while openai/spinningup's uses--batch-size=100by default.
Experiment results
To run benchmark experiments, see benchmark/sac.sh. Specifically, execute the following command:
| benchmark/sac.sh | |
|---|---|
1 2 3 4 5 6 7 | |
The table below compares the results of CleanRL's sac_continuous_action.py with the latest published results by the original authors of the SAC algorithm.
Info
Note that the results table above references the training episodic return for sac_continuous_action.py, the results of Soft Actor-Critic Algorithms and Applications reference evaluation episodic return obtained by running the policy in the deterministic mode.
| Environment | sac_continuous_action.py |
SAC: Algorithms and Applications @ 1M steps |
|---|---|---|
| HalfCheetah-v2 | 9634.89 ± 1423.73 | ~11,250 |
| Walker2d-v2 | 3591.45 ± 911.33 | ~4,800 |
| Hopper-v2 | 2310.46 ± 342.82 | ~3,250 |
| InvertedPendulum-v4 | 909.37 ± 55.66 | N/A |
| Humanoid-v4 | 4996.29 ± 686.40 | ~4500 |
| Pusher-v4 | -22.45 ± 0.51 | N/A |
Learning curves:
| benchmark/sac_plot.sh | |
|---|---|
1 2 3 4 5 6 7 8 9 | |
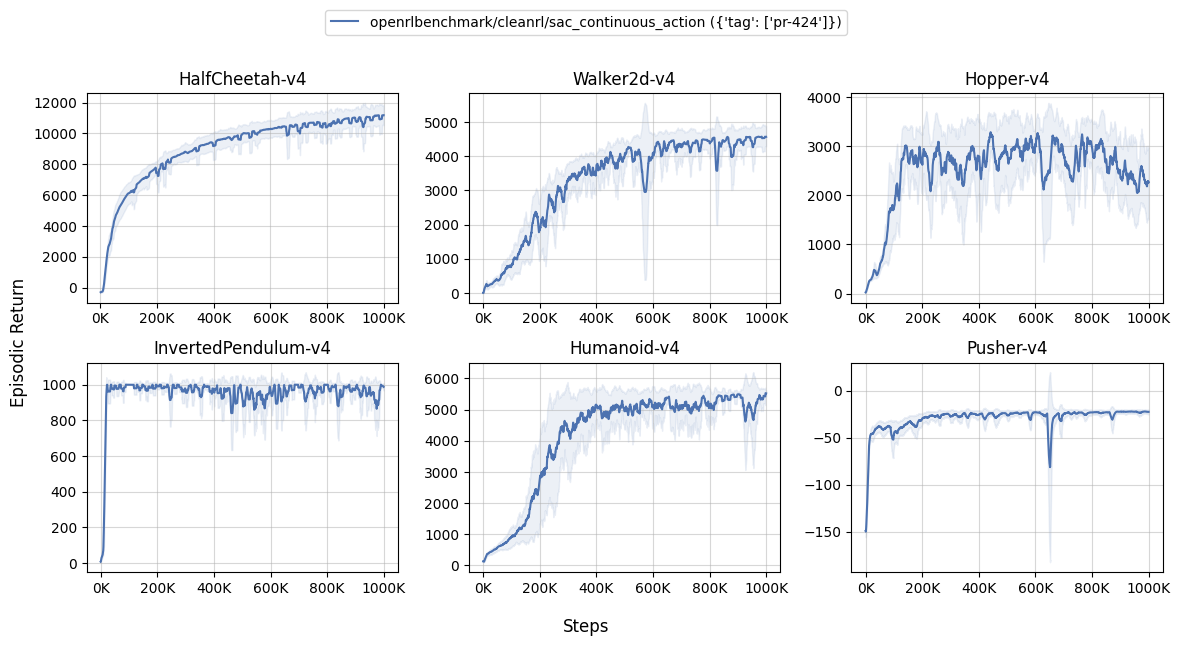
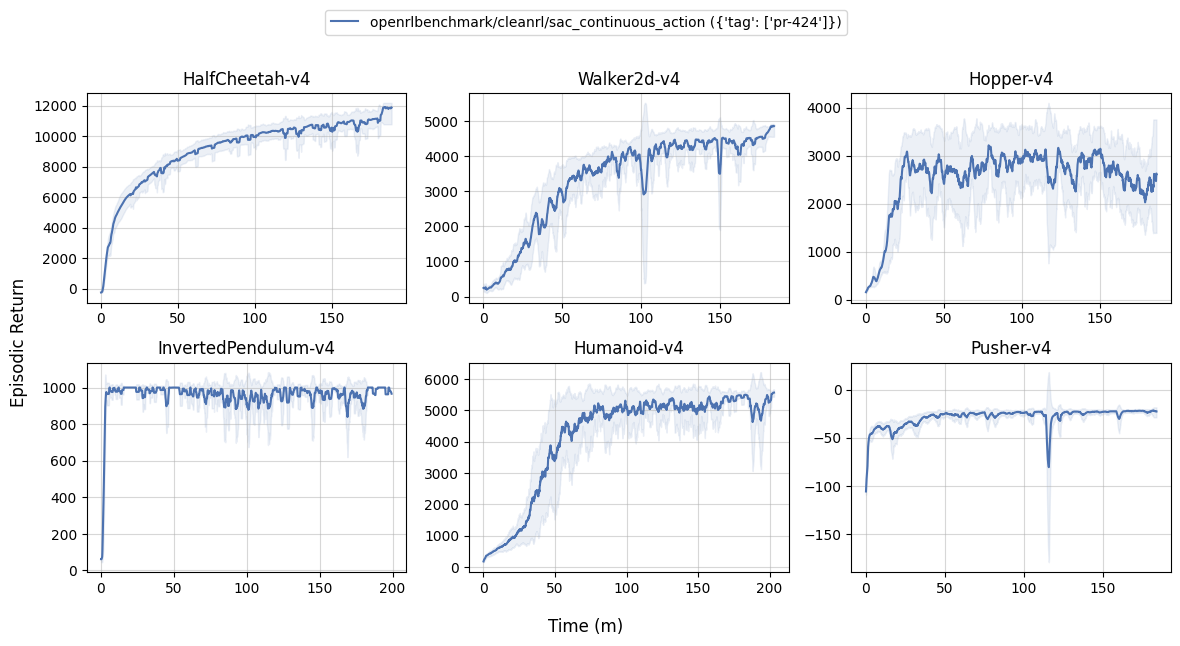
Tracked experiments and game play videos:
sac_atari.py
The sac_atari.py has the following features:
- For discrete action spaces.
- Works with the
Boxobservation space of low-level features. - Works with the
Discreteaction space. - Improved stability and wall-clock efficiency through updates only every n-th step.
- Supports automatic entropy coefficient \(\alpha\) tuning, enabled by default.
Usage for discrete action spaces
poetry install
poetry install -E atari
poetry run python cleanrl/sac_atari.py.py --env-id PongNoFrameskip-v4
poetry run python cleanrl/sac_atari.py.py --env-id PongNoFrameskip-v4 --autotune False --alpha 0.2
pip install -r requirements/requirements-atari.txt
python cleanrl/sac_atari.py.py --env-id PongNoFrameskip-v4
python cleanrl/sac_atari.py.py --env-id PongNoFrameskip-v4 --autotune False --alpha 0.2
Explanation of the logged metrics
The metrics logged by python cleanrl/sac_atari.py are the same as the ones logged by python cleanrl/sac_continuous_action.py (see the related docs). However, the computations for the objectives differ in some details highlighted below:
losses/qf1_loss,losses/qf2_loss: for each Soft Q-value network \(Q_{\theta_i}\), \(i \in \{1,2\}\), this metric holds the mean squared error (MSE) between the soft Q-value estimate \(Q_{\theta_i}(s, a)\) and the entropy regularized Bellman update target estimated as \(r_t + \gamma \, Q_{\theta_{i}^{'}}(s', a') + \alpha \, \mathcal{H} \big[ \pi(a' \vert s') \big]\).
SAC-discrete is able to exploit the discrete action space by using the full action distribution to calculate the Soft Q-targets instead of relying on a Monte Carlo approximation from a single Q-value. The new Soft Q-target is stated below with differences to the continuous SAC target highlighted in orange: $$ y = r(s, a) + \gamma \, {\color{orange}\pi (a | s^\prime)^{\mathsf T}} \Big(\min_{\theta_{1,2}} {\color{orange}Q_{\theta_i^{'}}(s')} - \alpha \, \log \pi( \cdot \vert s')\Big)~, $$
Note how in the discrete setting the Q-function \(Q_{\theta_i^{'}}(s')\) is a mapping \(Q:S \rightarrow \mathbb R^{|\mathcal A|}\) that only takes states as inputs and outputs Q-values for all actions. Using all this available information and additionally weighing the target by the corresponding action selection probability reduces variance of the gradient.
losses/actor_loss: Given the stochastic nature of the policy in SAC, the actor (or policy) objective is formulated so as to maximize the likelihood of actions \(a \sim \pi( \cdot \vert s)\) that would result in high Q-value estimate \(Q(s, a)\). Additionally, the policy objective encourages the policy to maintain its entropy high enough to help explore, discover, and capture multi-modal optimal policies.
SAC-discrete uses an action probability-weighted (highlighted in orange) objective given as:
Unlike for continuous action spaces, there is no need for the reparameterization trick due to using a Categorical policy. Similar to the critic objective, the Q-function \(Q_{\theta_i}(s)\) is a function from states to real numbers and does not require actions as inputs.
losses/alpha_loss: In the policy's objective defined above, the coefficient of the entropy bonus \(\alpha\) is kept fixed all across the training. As suggested by the authors in Section 5 of the Soft Actor-Critic And Applications paper, the original purpose of augmenting the standard reward with the entropy of the policy is to encourage exploration of not well enough explored states (thus high entropy). Conversely, for states where the policy has already learned a near-optimal policy, it would be preferable to reduce the entropy bonus of the policy, so that it does not become sub-optimal due to the entropy maximization incentive.
In SAC-discrete, it is possible to weigh the target for the entropy coefficient by the policy's action selection probabilities to reduce gradient variance. This is the same trick that was already used in the critic and actor objectives, with differences to the regular SAC objective marked in orange:
Since SAC-discrete uses a Categorical policy in a discrete action space, a different entropy target is required. The author uses the maximum entropy Categorical distribution (assigning uniform probability to all available actions) scaled by a factor of \(\tau~.\)
Implementation details
sac_atari.py uses the wrappers highlighted in the "9 Atari implementation details" in The 37 Implementation Details of Proximal Policy Optimization, which are as follows:
- The Use of
NoopResetEnv( common/atari_wrappers.py#L12) - The Use of
MaxAndSkipEnv( common/atari_wrappers.py#L97) - The Use of
EpisodicLifeEnv( common/atari_wrappers.py#L61) - The Use of
FireResetEnv( common/atari_wrappers.py#L41) - The Use of
WarpFrame(Image transformation) common/atari_wrappers.py#L134 - The Use of
ClipRewardEnv( common/atari_wrappers.py#L125) - The Use of
FrameStack( common/atari_wrappers.py#L188) - Shared Nature-CNN network for the policy and value functions ( common/policies.py#L157, common/models.py#L15-L26)
- Scaling the Images to Range [0, 1] ( common/models.py#L19)
Other noteworthy implementation details apart from the Atari wrapping are as follows:
-
sac_atari.pyinitializes the weights of its networks using He initialization (named after its author Kaiming He) from the paper "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification". The corresponding function in PyTorch iskaiming_normal_, its documentation can be found here. In essence, it means the weights of each layer are initialized according to a Normal distribution with mean \(\mu=0\) and\[ \sigma = \frac{\text{gain}}{\sqrt{\text{fan}}}~, \]where \(\text{fan}\) is the number of input neurons to the layer and \(\text{gain}\) is a constant set to \(\sqrt{2}\) for
ReLUlayers. -
sac_atari.pyuses the Adam2 optimizer with an increased \(\epsilon\)-parameter to improve its stability. This results in an increase in the denominator of the update rule:\[ \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} \]Here \(\hat{m}_t\) is the bias-corrected first moment and \(\hat{v}_t\) the bias-corrected second raw moment.
-
sac_atari.pyuses the action selection probabilities of the policy in multiple places to reduce the variance of gradient estimates. The target for the Soft Q-value estimate is weighted accordingly:# CRITIC training with torch.no_grad(): _, next_state_log_pi, next_state_action_probs = actor.get_action(data.next_observations) qf1_next_target = qf1_target(data.next_observations) qf2_next_target = qf2_target(data.next_observations) # we can use the action probabilities instead of MC sampling to estimate the expectation min_qf_next_target = next_state_action_probs * ( torch.min(qf1_next_target, qf2_next_target) - alpha * next_state_log_pi )A similar action-probability weighting can be used for the actor gradient:
_, log_pi, action_probs = actor.get_action(data.observations) with torch.no_grad(): qf1_values = qf1(data.observations) qf2_values = qf2(data.observations) min_qf_values = torch.min(qf1_values, qf2_values) # no need for reparameterization, the expectation can be calculated for discrete actions actor_loss = (action_probs * ((alpha * log_pi) - min_qf_values)).mean()Lastly, this variance reduction scheme is also used when automatic entropy tuning is enabled:
if args.autotune: # re-use action probabilities for temperature loss alpha_loss = (action_probs.detach() * (-log_alpha.exp() * (log_pi + target_entropy).detach())).mean() a_optimizer.zero_grad() alpha_loss.backward() a_optimizer.step() alpha = log_alpha.exp().item() -
sac_atari.pyuses--target-entropy-scale=0.89while the SAC-discrete paper uses--target-entropy-scale=0.98due to improved stability when training for more than 100k steps. Tuning this parameter to the environment at hand is advised and can lead to significant performance gains. -
sac_atari.pyperforms learning updates only on every \(n^{\text{th}}\) step. This leads to improved stability and prevents the agent's performance from degenerating during longer training runs.
Note the difference tosac_continuous_action.py:sac_atari.pyupdates every \(n^{\text{th}}\) environment step and does a single update of actor and critic on every update step.sac_continuous_action.pyupdates the critic every step and the actor every \(n^{\text{th}}\) step. It then compensates for the delayed actor updates by performing \(n\) actor update steps. -
sac_atari.pyhandles truncation and termination properly like (Mnih et al., 2015)3 by using SB3's replay buffer'shandle_timeout_termination=True.
Atari experiment results for SAC-discrete
Run benchmarks for benchmark/sac_atari.sh by executing:
The table below compares the results of CleanRL's sac_atari.py with the original paper results.
Info
Note that the results table above references the training episodic return for sac_atari.py without evaluation mode.
| Environment | sac_atari.py 100k steps |
SAC for Discrete Action Settings 100k steps | sac_atari.py 5M steps |
dqn_atari.py 10M steps |
|---|---|---|---|---|
| PongNoFrameskip-v4 | ~ -20.21 ± 0.62 | -20.98 ± 0.0 | ~19.24 ± 1.81 | 20.25 ± 0.41 |
| BreakoutNoFrameskip-v4 | ~2.33 ± 1.28 | - | ~343.66 ± 93.34 | 366.928 ± 39.89 |
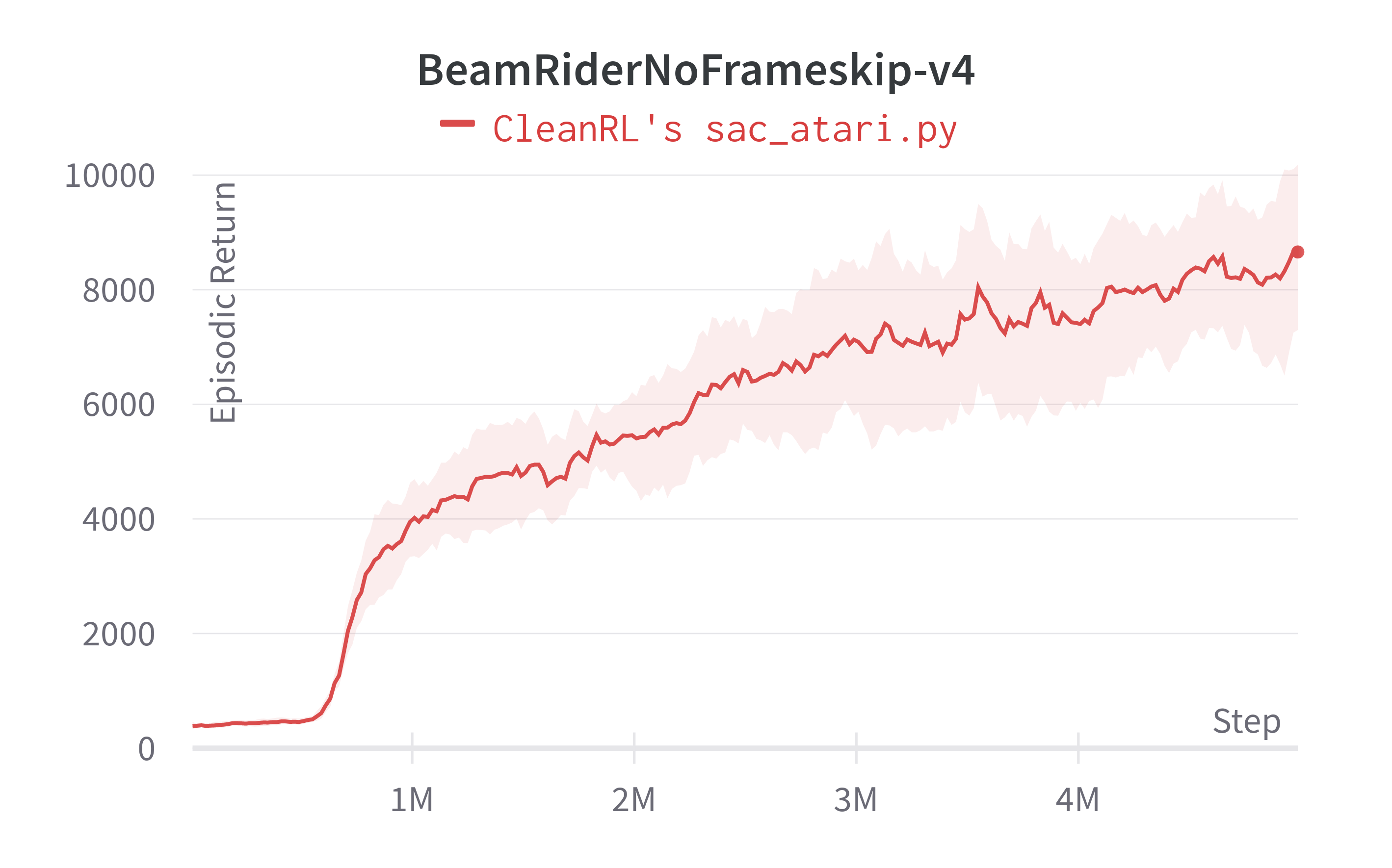
| BeamRiderNoFrameskip-v4 | ~396.15 ± 155.81 | 432.1 ± 44.0 | ~8658.97 ± 1554.66 | 6673.24 ± 1434.37 |
Learning curves:
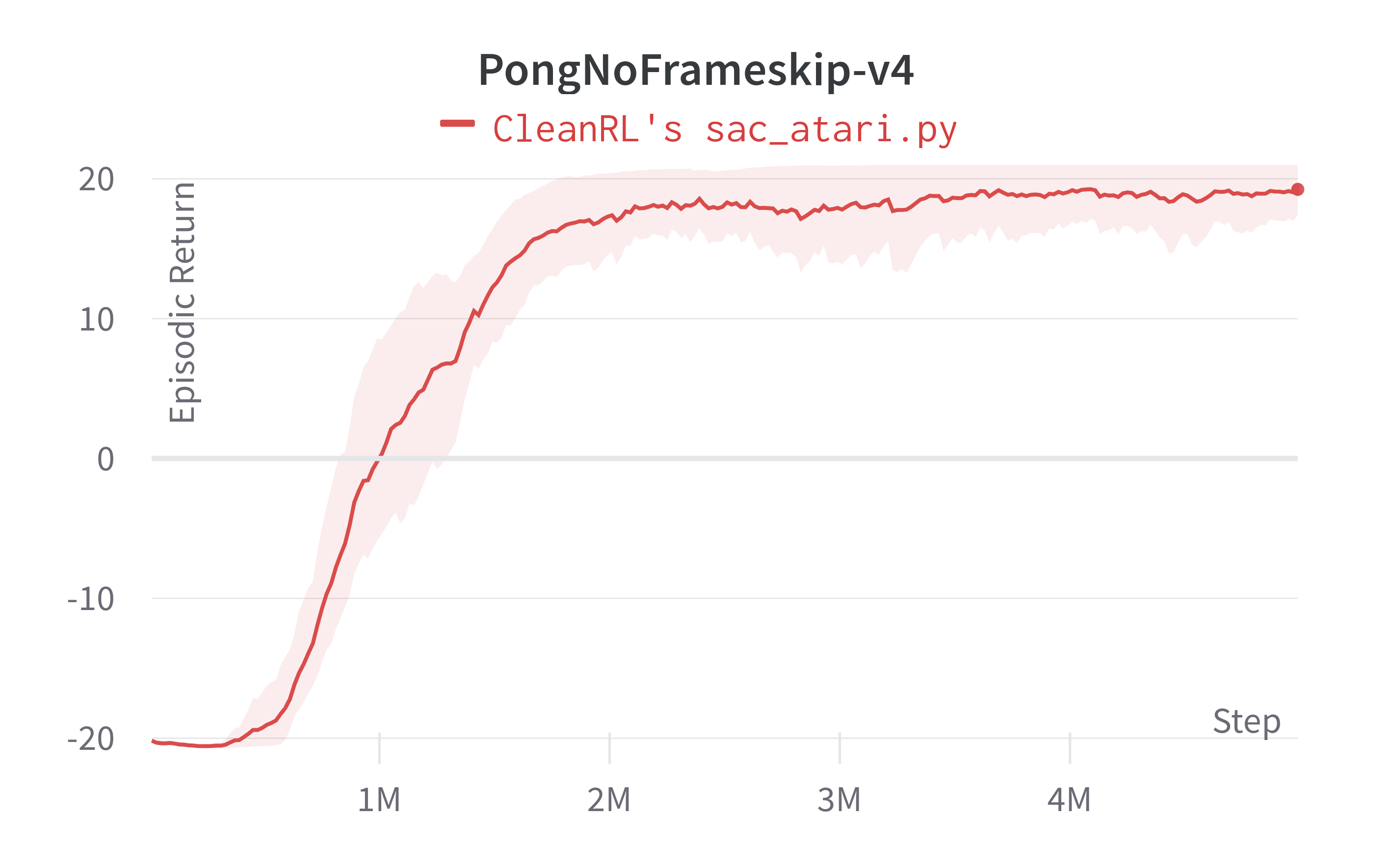
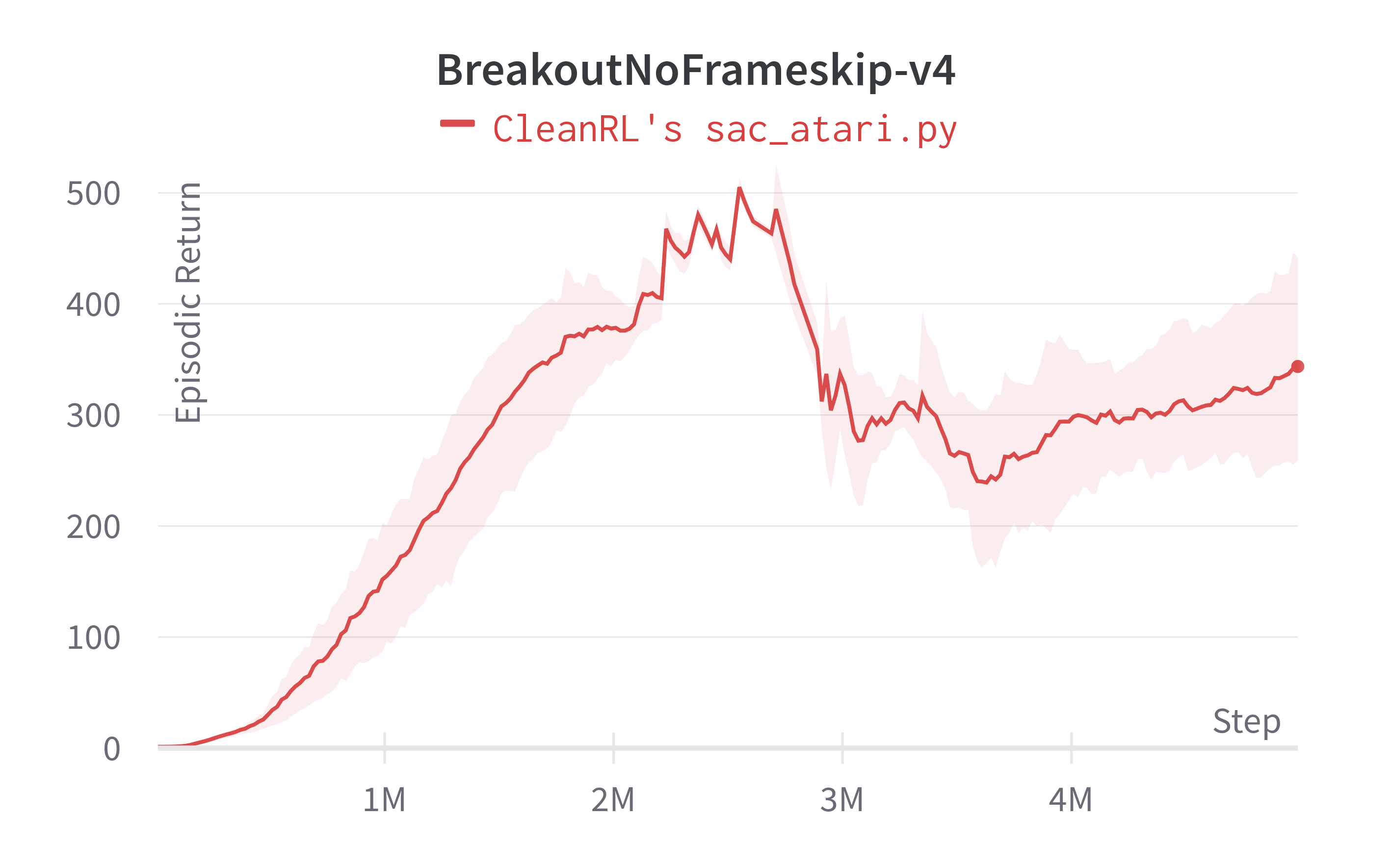
Tracked experiments:
-
Diederik P Kingma, Max Welling (2016). Auto-Encoding Variational Bayes. ArXiv, abs/1312.6114. https://arxiv.org/abs/1312.6114 ↩
-
Diederik P Kingma, Jimmy Lei Ba (2015). Adam: A Method for Stochastic Optimization. ArXiv, abs/1412.6980. https://arxiv.org/abs/1412.6980 ↩
-
Mnih, V., Kavukcuoglu, K., Silver, D. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015). https://doi.org/10.1038/nature14236 ↩