Deep Deterministic Policy Gradient (DDPG)
Overview
DDPG is a popular DRL algorithm for continuous control. It extends DQN to work with the continuous action space by introducing a deterministic actor that directly outputs continuous actions. DDPG also combines techniques from DQN, such as the replay buffer and target network.
Original paper:
Reference resources:
- sfujim/TD3
- Deep Deterministic Policy Gradient | Spinning Up in Deep RL
- ikostrikov/jaxrl (helpful reference when implemented
ddpg_continuous_action_jax.py)
Implemented Variants
| Variants Implemented | Description |
|---|---|
ddpg_continuous_action.py, docs |
For continuous action space |
ddpg_continuous_action_jax.py, docs |
For continuous action space |
Below is our single-file implementation of DDPG:
ddpg_continuous_action.py
The ddpg_continuous_action.py has the following features:
- For continuous action space
- Works with the
Boxobservation space of low-level features - Works with the
Box(continuous) action space
Usage
poetry install
poetry run python cleanrl/ddpg_continuous_action.py --help
poetry install -E mujoco
poetry run python cleanrl/ddpg_continuous_action.py --env-id Hopper-v4
python cleanrl/ddpg_continuous_action.py --help
pip install -r requirements/requirements-mujoco.txt
python cleanrl/ddpg_continuous_actions.py --env-id Hopper-v4
Explanation of the logged metrics
Running python cleanrl/ddpg_continuous_action.py will automatically record various metrics such as actor or value losses in Tensorboard. Below is the documentation for these metrics:
charts/episodic_return: episodic return of the gamecharts/SPS: number of steps per second-
losses/qf1_loss: the mean squared error (MSE) between the Q values at timestep \(t\) and the Bellman update target estimated using the reward \(r_t\) and the Q values at timestep \(t+1\), thus minimizing the one-step temporal difference. Formally, it can be expressed by the equation below. $$ J(\theta^{Q}) = \mathbb{E}_{(s,a,r,s') \sim \mathcal{D}} \big[ (Q(s, a) - y)^2 \big], $$ with the Bellman update target \(y = r + \gamma \, Q^{'}(s', a')\), where \(a' \sim \mu^{'}(s')\), and the replay buffer \(\mathcal{D}\). -
losses/actor_loss: implemented as-qf1(data.observations, actor(data.observations)).mean(); it is the negative average Q values calculated based on the 1) observations and the 2) actions computed by the actor based on these observations. By minimizingactor_loss, the optimizer updates the actors parameter using the following gradient (Lillicrap et al., 2016, Algorithm 1)1:
losses/qf1_values: implemented asqf1(data.observations, data.actions).view(-1), it is the average Q values of the sampled data in the replay buffer; useful when gauging if under or over estimation happens.
Implementation details
Our ddpg_continuous_action.py is based on the OurDDPG.py from sfujim/TD3, which presents the the following implementation difference from (Lillicrap et al., 2016)1:
-
ddpg_continuous_action.pyuses a gaussian exploration noise \(\mathcal{N}(0, 0.1)\), while (Lillicrap et al., 2016)1 uses Ornstein-Uhlenbeck process with \(\theta=0.15\) and \(\sigma=0.2\). -
ddpg_continuous_action.pyruns the experiments using theopenai/gymMuJoCo environments, while (Lillicrap et al., 2016)1 uses their proprietary MuJoCo environments. -
ddpg_continuous_action.pyuses the following architecture:while (Lillicrap et al., 2016, see Appendix 7 EXPERIMENT DETAILS)1 uses the following architecture (difference highlighted):class QNetwork(nn.Module): def __init__(self, env): super().__init__() self.fc1 = nn.Linear(np.array(env.single_observation_space.shape).prod() + np.prod(env.single_action_space.shape), 256) self.fc2 = nn.Linear(256, 256) self.fc3 = nn.Linear(256, 1) def forward(self, x, a): x = torch.cat([x, a], 1) x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = self.fc3(x) return x class Actor(nn.Module): def __init__(self, env): super().__init__() self.fc1 = nn.Linear(np.array(env.single_observation_space.shape).prod(), 256) self.fc2 = nn.Linear(256, 256) self.fc_mu = nn.Linear(256, np.prod(env.single_action_space.shape)) # action rescaling self.register_buffer( "action_scale", torch.tensor((env.action_space.high - env.action_space.low) / 2.0, dtype=torch.float32) ) self.register_buffer( "action_bias", torch.tensor((env.action_space.high + env.action_space.low) / 2.0, dtype=torch.float32) ) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = torch.tanh(self.fc_mu(x)) return x * self.action_scale + self.action_biasclass QNetwork(nn.Module): def __init__(self, env): super(QNetwork, self).__init__() self.fc1 = nn.Linear(p.array(env.single_observation_space.shape).prod() + np.prod(env.single_action_space.shape), 400) self.fc2 = nn.Linear(400 + np.prod(env.single_action_space.shape), 300) self.fc3 = nn.Linear(300, 1) def forward(self, x, a): x = F.relu(self.fc1(x)) x = torch.cat([x, a], 1) x = F.relu(self.fc2(x)) x = self.fc3(x) return x class Actor(nn.Module): def __init__(self, env): super(Actor, self).__init__() self.fc1 = nn.Linear(np.array(env.single_observation_space.shape).prod(), 400) self.fc2 = nn.Linear(400, 300) self.fc_mu = nn.Linear(300, np.prod(env.single_action_space.shape)) # action rescaling self.register_buffer( "action_scale", torch.tensor((env.action_space.high - env.action_space.low) / 2.0, dtype=torch.float32) ) self.register_buffer( "action_bias", torch.tensor((env.action_space.high + env.action_space.low) / 2.0, dtype=torch.float32) ) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = torch.tanh(self.fc_mu(x)) return x * self.action_scale + self.action_bias -
ddpg_continuous_action.pyuses the following learning rates:while (Lillicrap et al., 2016, see Appendix 7 EXPERIMENT DETAILS)1 uses the following learning rates:q_optimizer = optim.Adam(list(qf1.parameters()), lr=3e-4) actor_optimizer = optim.Adam(list(actor.parameters()), lr=3e-4)q_optimizer = optim.Adam(list(qf1.parameters()), lr=1e-4) actor_optimizer = optim.Adam(list(actor.parameters()), lr=1e-3) -
ddpg_continuous_action.pyuses--batch-size=256 --tau=0.005, while (Lillicrap et al., 2016, see Appendix 7 EXPERIMENT DETAILS)1 uses--batch-size=64 --tau=0.001 -
ddpg_continuous_action.pyalso adds support for handling continuous environments where the lower and higher bounds of the action space are not \([-1,1]\), or are asymmetric. The case where the bounds are not \([-1,1]\) is handled inDDPG.py(Fujimoto et al., 2018)2 as follows:On the other hand, inclass Actor(nn.Module): ... def forward(self, state): a = F.relu(self.l1(state)) a = F.relu(self.l2(a)) return self.max_action * torch.tanh(self.l3(a)) # Scale from [-1,1] to [-action_high, action_high]CleanRL's ddpg_continuous_action.py, the mean and the scale of the the action space are computed asaction_biasandaction_scalerespectively. Those scalars are in turn used to scale the output of atanhactivation function in the actor to the original action space range:class Actor(nn.Module): def __init__(self, env): ... # action rescaling self.register_buffer( "action_scale", torch.tensor((env.action_space.high - env.action_space.low) / 2.0, dtype=torch.float32) ) self.register_buffer( "action_bias", torch.tensor((env.action_space.high + env.action_space.low) / 2.0, dtype=torch.float32) ) def forward(self, x): x = F.relu(self.fc1(x)) x = F.relu(self.fc2(x)) x = torch.tanh(self.fc_mu(x)) return x * self.action_scale + self.action_bias # Scale from [-1,1] to [-action_low, action_high]
Additionally, when drawing exploration noise that is added to the actions produced by the actor, CleanRL's ddpg_continuous_action.py centers the distribution the sampled from at action_bias, and the scale of the distribution is set to action_scale * exploration_noise.
Info
Note that Humanoid-v2, InvertedPendulum-v2, Pusher-v2 have action space bounds that are not the standard [-1, 1]. See below.
Ant-v2 Observation space: Box(-inf, inf, (111,), float64) Action space: Box(-1.0, 1.0, (8,), float32)
HalfCheetah-v2 Observation space: Box(-inf, inf, (17,), float64) Action space: Box(-1.0, 1.0, (6,), float32)
Hopper-v2 Observation space: Box(-inf, inf, (11,), float64) Action space: Box(-1.0, 1.0, (3,), float32)
Humanoid-v2 Observation space: Box(-inf, inf, (376,), float64) Action space: Box(-0.4, 0.4, (17,), float32)
InvertedDoublePendulum-v2 Observation space: Box(-inf, inf, (11,), float64) Action space: Box(-1.0, 1.0, (1,), float32)
InvertedPendulum-v2 Observation space: Box(-inf, inf, (4,), float64) Action space: Box(-3.0, 3.0, (1,), float32)
Pusher-v2 Observation space: Box(-inf, inf, (23,), float64) Action space: Box(-2.0, 2.0, (7,), float32)
Reacher-v2 Observation space: Box(-inf, inf, (11,), float64) Action space: Box(-1.0, 1.0, (2,), float32)
Swimmer-v2 Observation space: Box(-inf, inf, (8,), float64) Action space: Box(-1.0, 1.0, (2,), float32)
Walker2d-v2 Observation space: Box(-inf, inf, (17,), float64) Action space: Box(-1.0, 1.0, (6,), float32)
Experiment results
To run benchmark experiments, see benchmark/ddpg.sh. Specifically, execute the following command:
| benchmark/ddpg.sh | |
|---|---|
1 2 3 4 5 6 7 | |
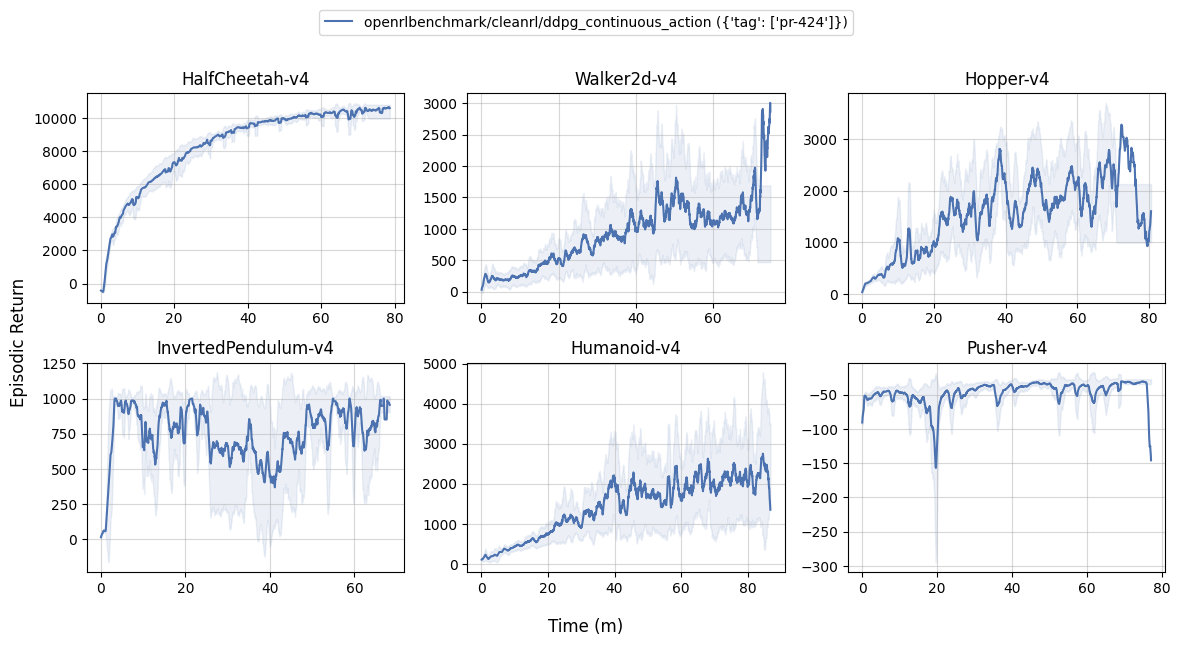
Below are the average episodic returns for ddpg_continuous_action.py (3 random seeds). To ensure the quality of the implementation, we compared the results against (Fujimoto et al., 2018)2.
| Environment | ddpg_continuous_action.py |
OurDDPG.py (Fujimoto et al., 2018, Table 1)2 |
DDPG.py using settings from (Lillicrap et al., 2016)1 in (Fujimoto et al., 2018, Table 1)2 |
|---|---|---|---|
| HalfCheetah-v4 | 10374.07 ± 157.37 | 8577.29 | 3305.60 |
| Walker2d-v4 | 1240.16 ± 390.10 | 3098.11 | 1843.85 |
| Hopper-v4 | 1576.78 ± 818.98 | 1860.02 | 2020.46 |
| InvertedPendulum-v4 | 642.68 ± 69.56 | 1000.00 ± 0.00 | |
| Humanoid-v4 | 1699.56 ± 694.22 | not available | |
| Pusher-v4 | -77.30 ± 38.78 | not available |
Info
Note that ddpg_continuous_action.py uses gym MuJoCo v4 environments while OurDDPG.py (Fujimoto et al., 2018)2 uses the gym MuJoCo v1 environments.
Also note the performance of our ddpg_continuous_action.py seems to be worse than the reference implementation on Walker2d and Hopper. This is likely due to openai/gym#938. We would have a hard time reproducing gym MuJoCo v1 environments because they have been long deprecated.
One other thing could cause the performance difference: the original code reported the average episodic return using determinisitc evaluation (i.e., without exploration noise), see sfujim/TD3/main.py#L15-L32, whereas we reported the episodic return during training and the policy gets updated between environments steps.
Learning curves:
| benchmark/ddpg_plot.sh | |
|---|---|
1 2 3 4 5 6 7 8 9 | |

ddpg_continuous_action_jax.py
The ddpg_continuous_action_jax.py has the following features:
- Uses Jax, Flax, and Optax instead of
torch. ddpg_continuous_action_jax.py is roughly 2.5-4x faster than ddpg_continuous_action.py - For continuous action space
- Works with the
Boxobservation space of low-level features - Works with the
Box(continuous) action space
Usage
poetry install
poetry install -E "mujoco jax"
poetry run python cleanrl/ddpg_continuous_action_jax.py --help
poetry run python cleanrl/ddpg_continuous_action_jax.py --env-id Hopper-v4
poetry install -E mujoco_py # only works in Linux
poetry run python cleanrl/ddpg_continuous_action_jax.py --env-id Hopper-v2
pip install -r requirements/requirements-mujoco.txt
pip install -r requirements/requirements-jax.txt
python cleanrl/ddpg_continuous_action_jax.py --help
python cleanrl/ddpg_continuous_action_jax.py --env-id Hopper-v4
pip install -r requirements/requirements-mujoco_py.txt # only works in Linux
python cleanrl/ddpg_continuous_action_jax.py --env-id Hopper-v2
Warning
Note that JAX does not work in Windows . The official docs recommends using Windows Subsystem for Linux (WSL) to install JAX.
Explanation of the logged metrics
See related docs for ddpg_continuous_action.py.
Implementation details
See related docs for ddpg_continuous_action.py.
Experiment results
To run benchmark experiments, see benchmark/ddpg.sh. Specifically, execute the following command:
| benchmark/ddpg.sh | |
|---|---|
1 2 3 4 5 6 7 8 | |
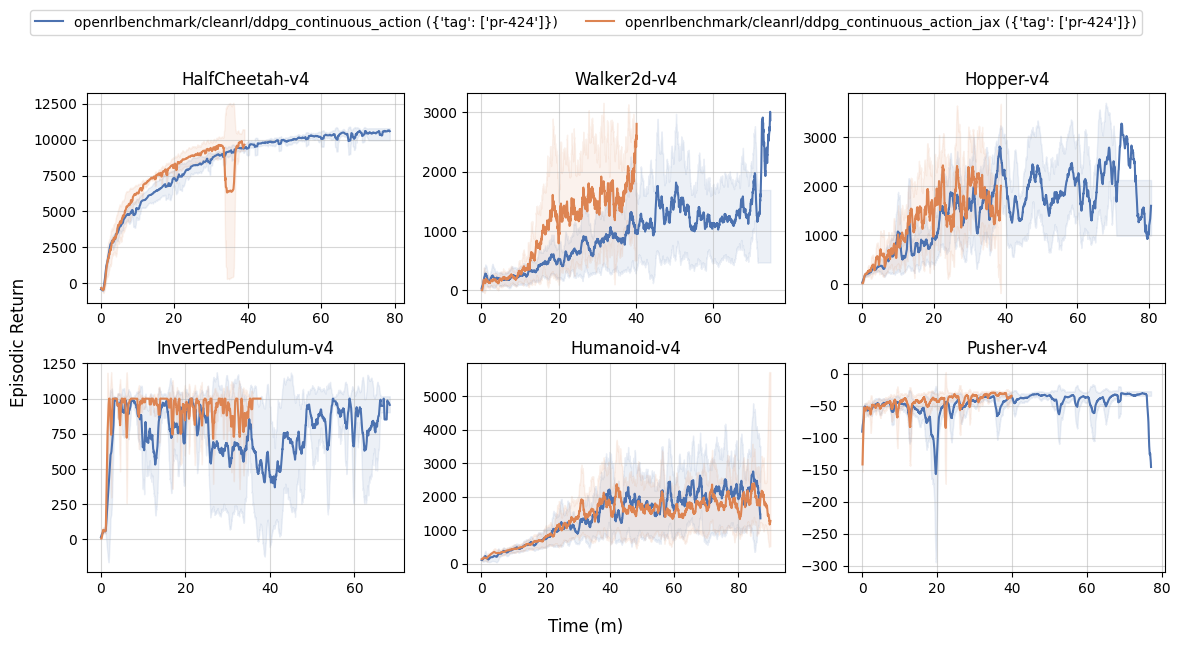
Below are the average episodic returns for ddpg_continuous_action_jax.py (3 random seeds).
| openrlbenchmark/cleanrl/ddpg_continuous_action ({'tag': ['pr-424']}) | openrlbenchmark/cleanrl/ddpg_continuous_action_jax ({'tag': ['pr-424']}) | |
|---|---|---|
| HalfCheetah-v4 | 10374.07 ± 157.37 | 8638.60 ± 1954.46 |
| Walker2d-v4 | 1240.16 ± 390.10 | 1427.23 ± 104.91 |
| Hopper-v4 | 1576.78 ± 818.98 | 1208.52 ± 659.22 |
| InvertedPendulum-v4 | 642.68 ± 69.56 | 804.30 ± 87.60 |
| Humanoid-v4 | 1699.56 ± 694.22 | 1513.61 ± 248.60 |
| Pusher-v4 | -77.30 ± 38.78 | -38.56 ± 4.47 |
Learning curves:
| benchmark/ddpg_plot.sh | |
|---|---|
1 2 3 4 5 6 7 8 9 10 | |

Info
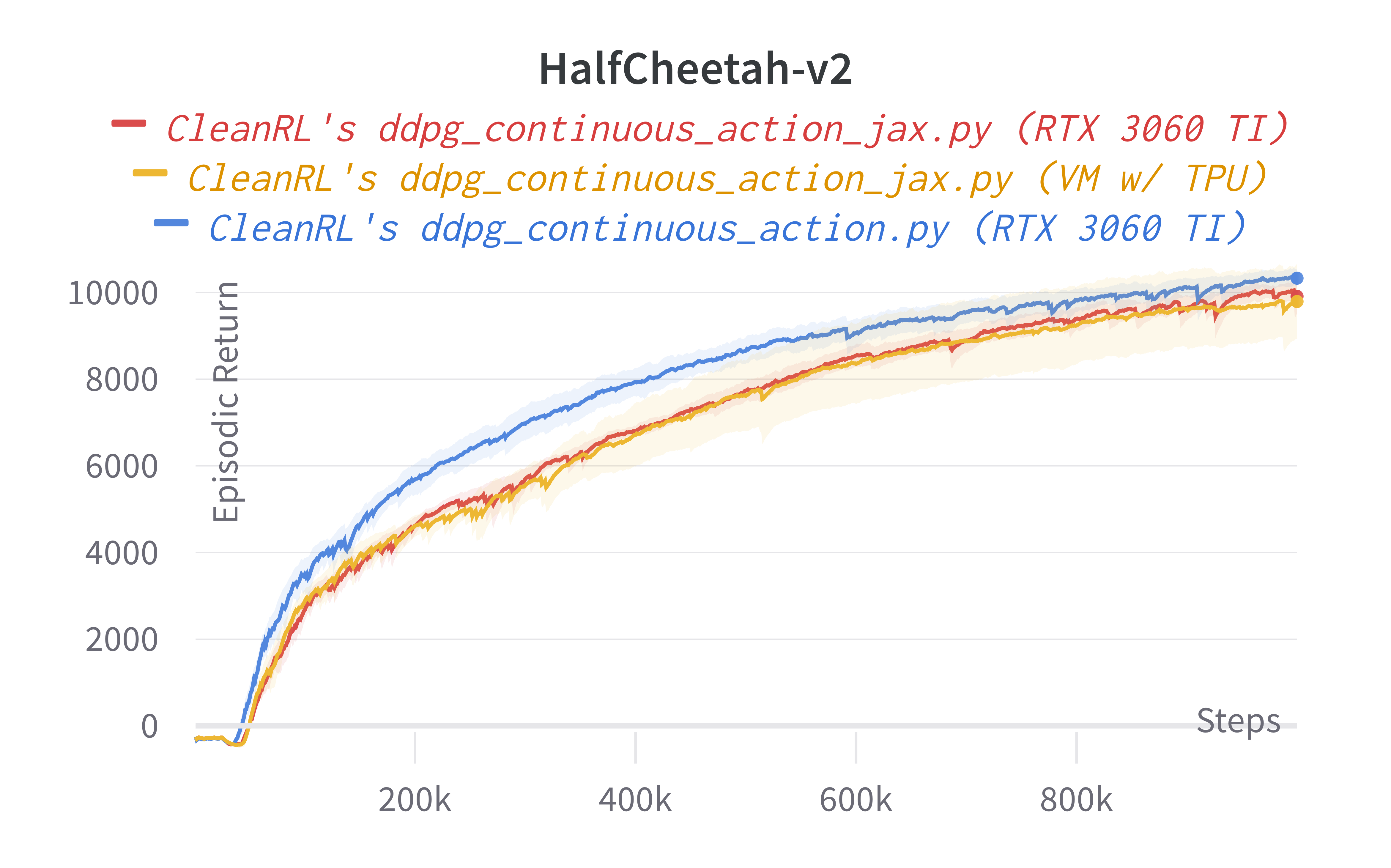
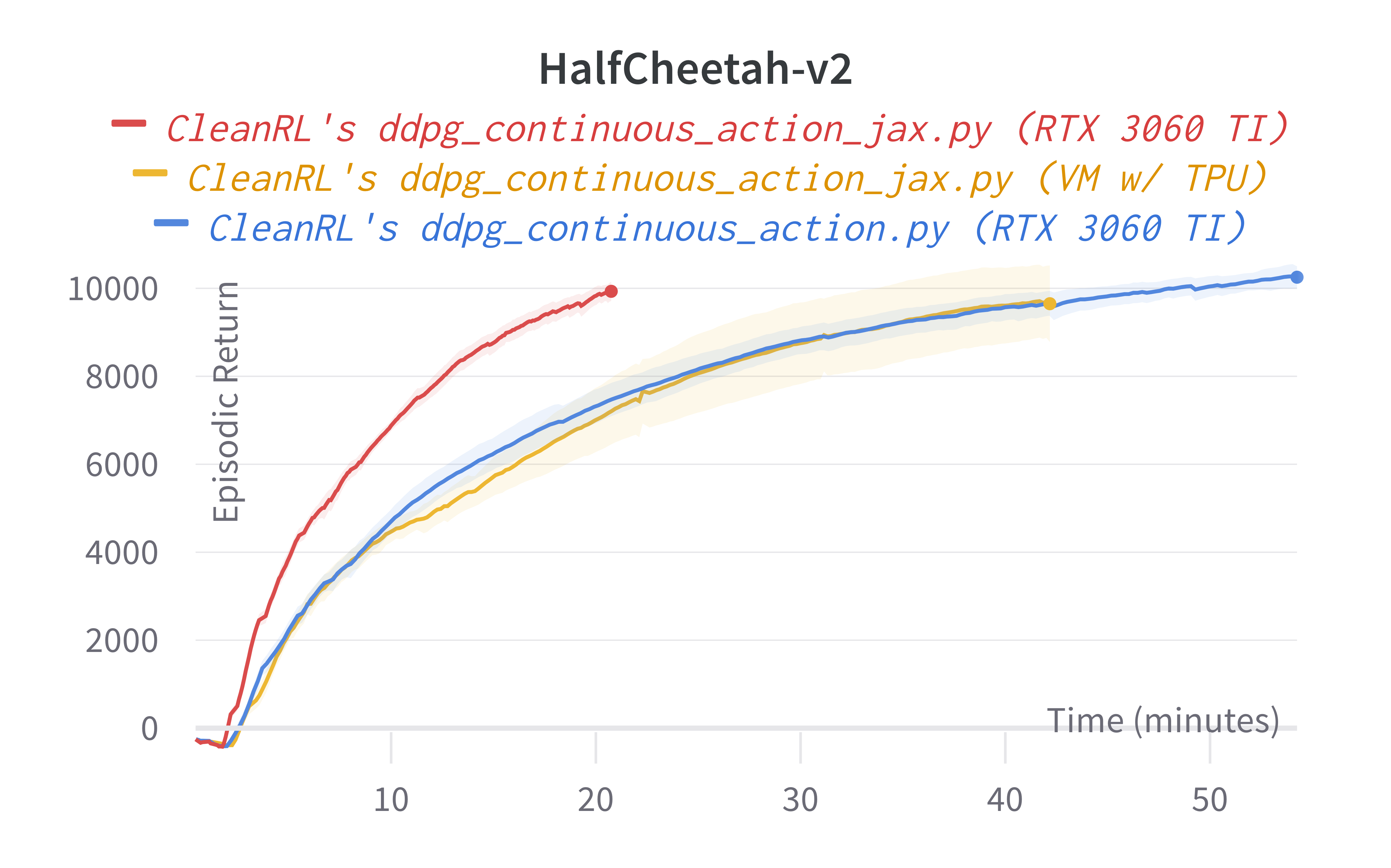
These are some previous experiments with TPUs. Note the results are very similar to the ones above, but the runtime can be different due to different hardware used.
Note that the experiments were conducted on different hardwares, so your mileage might vary. This inconsistency is because 1) re-running expeirments on the same hardware is computationally expensive and 2) requiring the same hardware is not inclusive nor feasible to other contributors who might have different hardwares.
That said, we roughly expect to see a 2-4x speed improvement from using ddpg_continuous_action_jax.py under the same hardware. And if you disable the --capture_video overhead, the speed improvement will be even higher.
| Environment | ddpg_continuous_action_jax.py (RTX 3060 TI) |
ddpg_continuous_action_jax.py (VM w/ TPU) |
ddpg_continuous_action.py (RTX 3060 TI) |
OurDDPG.py (Fujimoto et al., 2018, Table 1)2 |
|---|---|---|---|---|
| HalfCheetah | 9592.25 ± 135.10 | 9125.06 ± 1477.58 | 10210.57 ± 196.22 | 8577.29 |
| Walker2d | 1083.15 ± 567.65 | 1303.82 ± 448.41 | 1661.14 ± 250.01 | 3098.11 |
| Hopper | 1275.28 ± 209.60 | 1145.05 ± 41.95 | 1007.44 ± 148.29 | 1860.02 |
Learning curves:
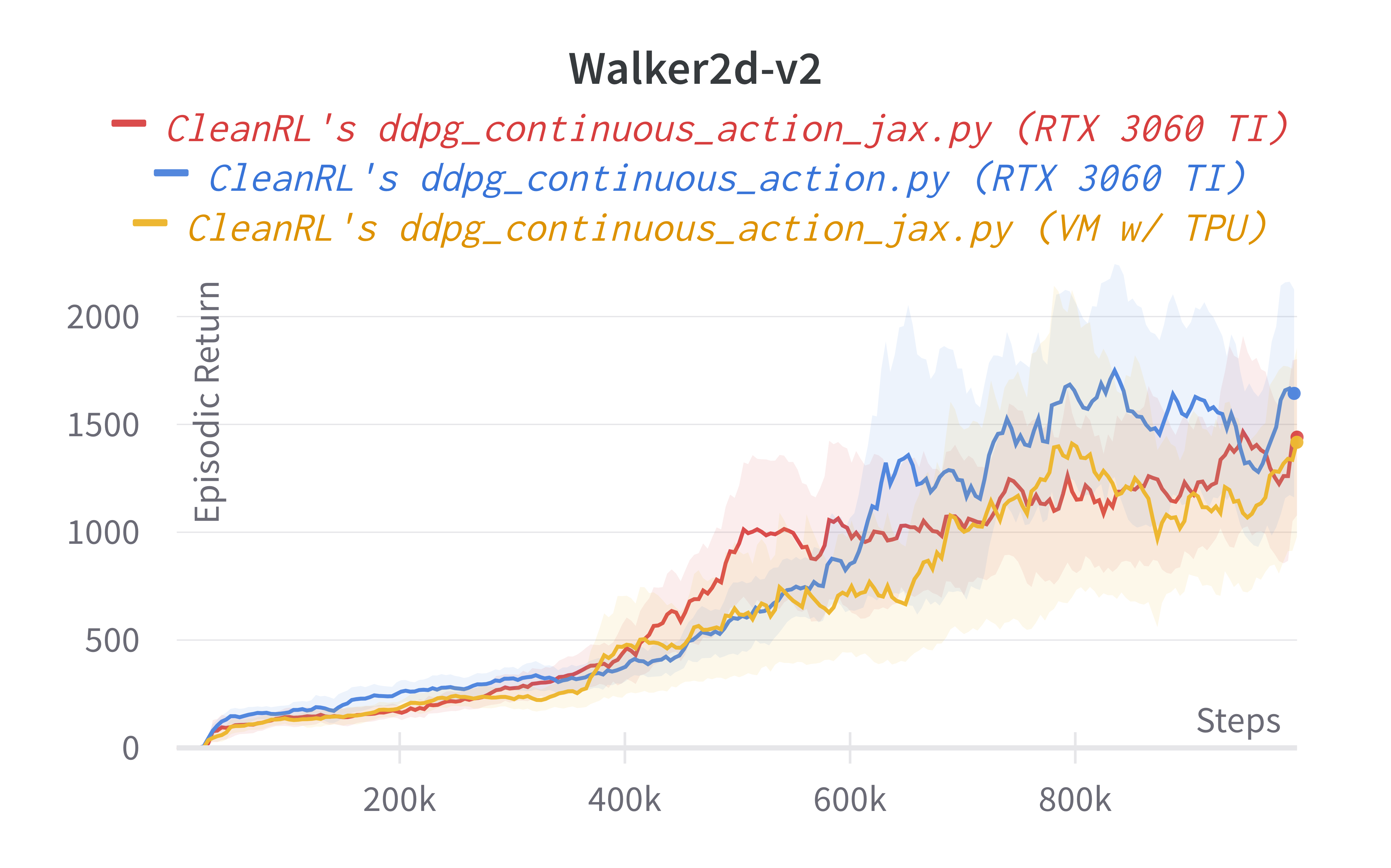
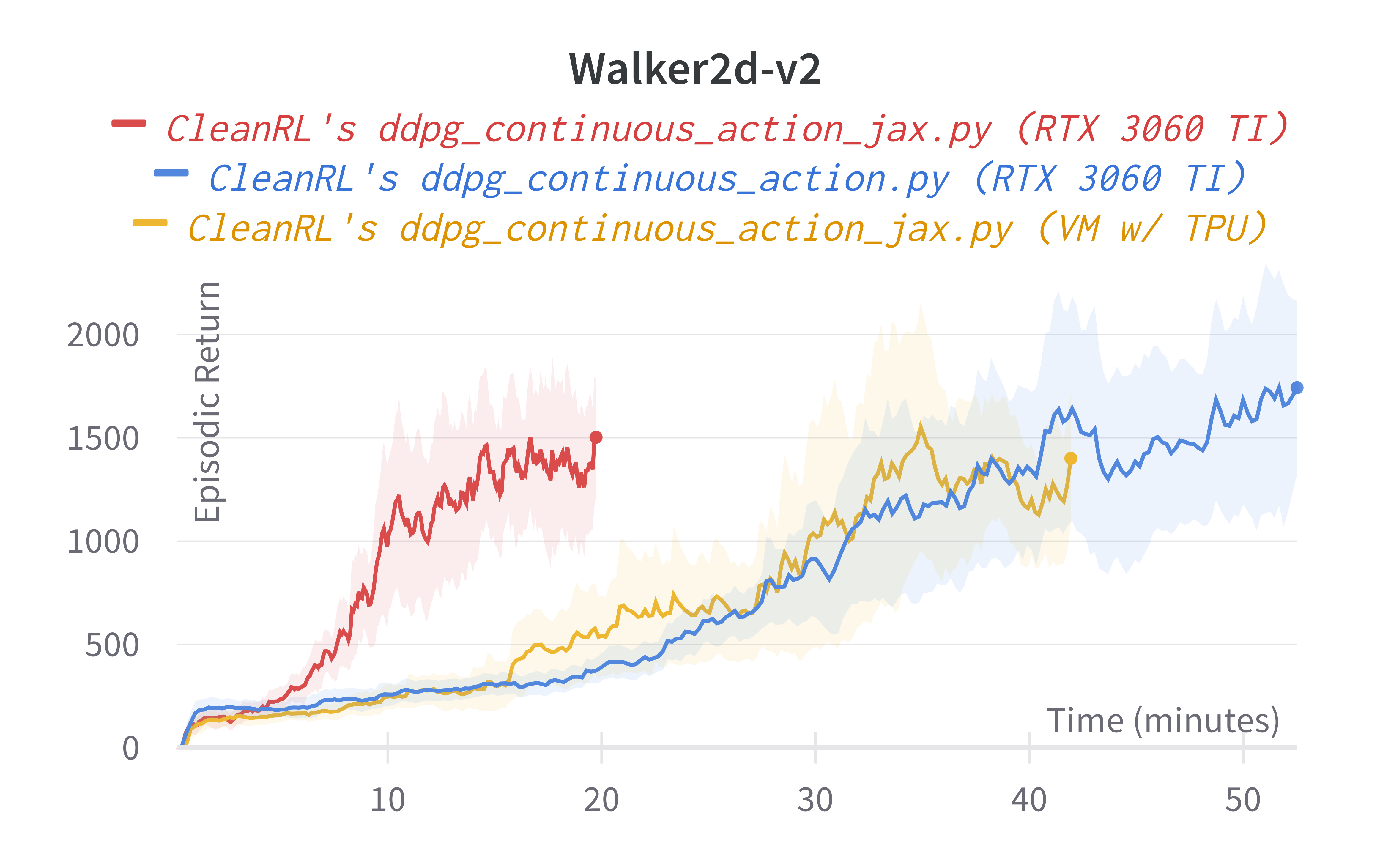
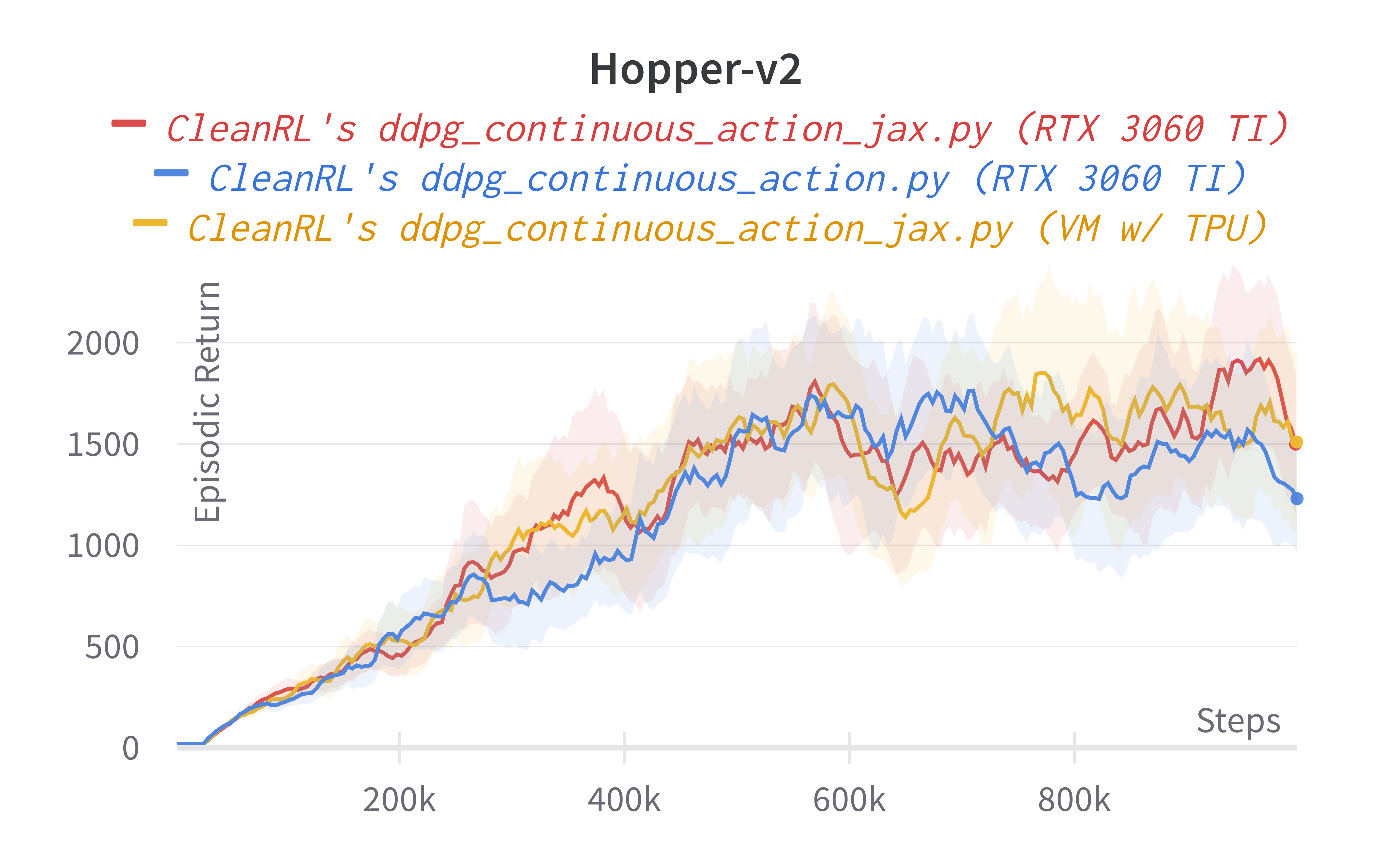

Tracked experiments and game play videos:
-
Lillicrap, T.P., Hunt, J.J., Pritzel, A., Heess, N.M., Erez, T., Tassa, Y., Silver, D., & Wierstra, D. (2016). Continuous control with deep reinforcement learning. CoRR, abs/1509.02971. https://arxiv.org/abs/1509.02971 ↩↩↩↩↩↩↩↩
-
Fujimoto, S., Hoof, H.V., & Meger, D. (2018). Addressing Function Approximation Error in Actor-Critic Methods. ArXiv, abs/1802.09477. https://arxiv.org/abs/1802.09477 ↩↩↩↩↩↩